Adattudományt tanulok szabadidőmben, és természetesen a pandas, numpy és matplotlib eszköztárainak felfedezésével kezdtem. Egy pár hét tanulás után, melyet egyébként egy online platformon keresztül végzek, szerettem volna összedobni egy egyszerű kis projektet, hogy lássam, hol is tartok.
Kutattam érdekes adathalmazok után az interneten, és meg is találtam az ötöslottó eredményeit, melyet hetente, a sorsolások után frissítenek. Az adathalmazban megtalálhatóak a nyerőszámok, illetve a nyertesek és nyereményeik kategóriánként (kettes, hármas, négyes vagy ötös).
Jupyter Notebook segítségével végeztem a minimális adattisztítást és az elemzéseket, de készítettem egy szebb formátumú riportot az eredményekről.
A notebook fájl megtalálható itt, a riport pedig itt.
Egy jól kinéző riportot szerettem volna készíteni, nem feledve azt, hogy ne csak számokat dobjak az olvasó elé, hanem inkább egy teljes történetet adjak át. Jah, és jó tudni, hogy a lottó 2017-ben volt 60 éves! :)

Tudva azt, hogy sok ember a saját szerencseszámaival játszik, legyenek azok a családi szülinapok, házszámok, stb, próbáltam néhány egyéb stratégiát összegyűjteni és elemezni hatékonyságukat:
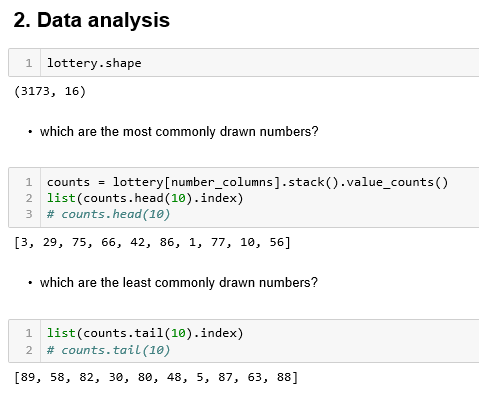
- leggyakrabban húzott számok
- legritkábban húzott számok
- legrégebb óta nem húzott számok

Kíváncsi voltam természetesen a telitalálatos nyereményekre is, de főként arra, hogy az évek során hogyan növekedtek a nyeremények. Szerencsétlenségemre az adathalmazban csak 1998 óta vannak erre vonatkozó információk.
Néhány érdekes adat kiesett ebből a projektből, és remélem, hogy többeknek is érdekes adatokkal tudtam szolgálni. Talán még pár embert ahhoz is hozzásegítetek, hogy egy nagyobb összeget tudjon nyerni egy másfajta stratégiát választva!
Ha bármilyen hibát, javaslatot, ötletet vagy csak visszajelzést adnál, akkor kérlek jelezd hozzászólásként, vagy írj ide: leah [kukac] floppylab [pont] com
# adathalmaz: itt (2018. 01. 01.) és eredetileg innen (hetente frissítve)
# kapcsolat: leah [at] floppylab [dot] com


